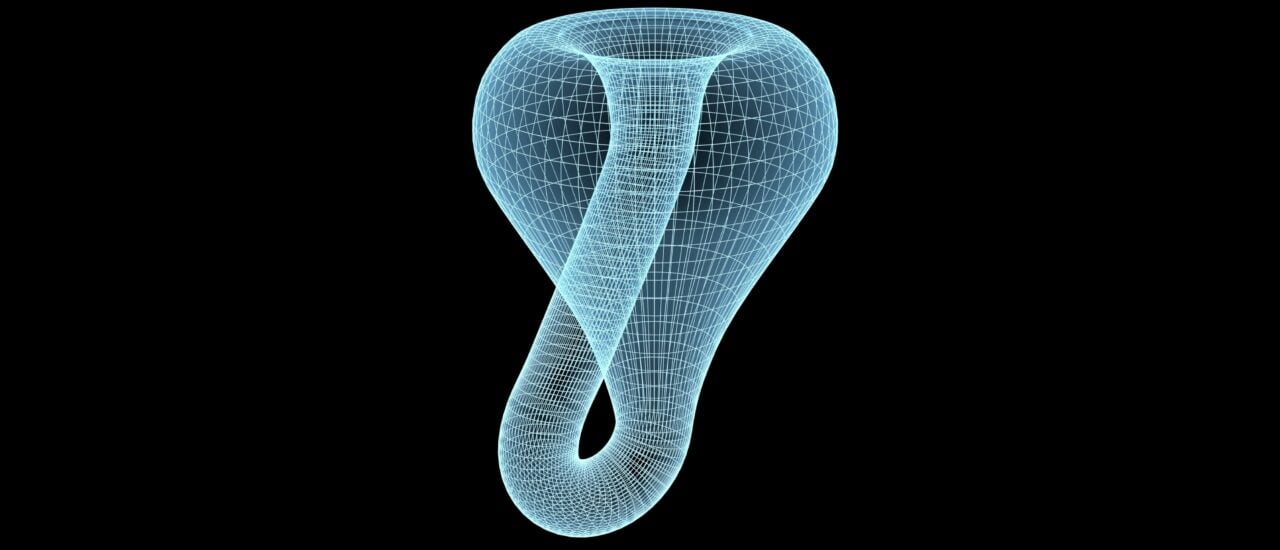
Leipzig, 11. Juni 1881. Ein Mann sitzt über seinen Schreibtisch gebeugt. Dunkles volles Haar, dichter Bart. Er sieht ziemlich jung aus, fast noch wie ein Student. Wären da nicht der formelle Anzug und die schwarze glänzende Fliege. Seit zehn Jahren schon ist er Professor, seit er 23 Jahre alt ist. Jetzt noch schnell die neuesten Artikel zur Mathematik aus Frankreich lesen, und dann ist aber auch Feierabend. Aber warte, was stand da gerade? Der Mann liest die Überschrift zweimal, dann nochmal und nochmal. Aber nein, er hat sich nicht verlesen: Sur les fonctions fuchsiennes – über die fuchsischen Funktionen. Die fuchsischen Funktionen. Den Fame für diese Funktion, die kriegt ausgerechnet Lazarus Fuchs, dieser mittelmäßige Typ aus Berlin. Was ist mit Schwarz? Was ist mit Riemann? Und was bitte ist mit ihm selbst? Dann nimmt er einen Stift und da, wo Fuchs steht, da schreibt er seinen eigenen Namen hin. Das ist die Geschichte von Felix Klein. Hallo und herzlich willkommen zu einer neuen Geschichte aus der Mathematik. Ich bin Carolin Breitschädel, ich hoste diesen Podcast, und mit mir hier im Studio ist Manon Bischoff, Mathe-Redakteurin von Spektrum der Wissenschaft. Hallo Manon, schön, dass du da bist. Hi Caro, schön, dass ich hier sein kann. Und natürlich ist auch unser Mann für die Geschichten da: Demian Nowel. Groß! Hallo Demian, schön, dass du da bist. Hallihallo, immer wieder schön. Und ein kleines Sorry schon mal vorab an unsere HörerInnen: Wir werden in dieser Folge einige Namen von Mathematikern droppen, ohne die dann groß weiter einzuordnen. Und ich bin echt kein Fan von Name-Dropping normalerweise, aber dieses Mal geht es einfach nicht anders, weil wir erzählen heute nämlich die Geschichte von Felix Klein. Und Felix Klein ist eben nicht nur ein sehr guter Mathematiker, er ist vor allem auch ein extrem erfolgreicher Networker. Es gibt wahrscheinlich niemanden in der deutschen Mathe-Community um 1900, den Felix Klein nicht kennt. Also Felix Klein kennt quasi alle Mathematiker seiner Zeit, und alle kennen Felix Klein. Was aber nicht heißt, dass alle ihn mögen. Es gibt nämlich zu dieser Zeit so eine Art Game of Thrones unter den mathematischen Denkschulen, und Felix Klein, der steckt mittendrin. Bevor wir da gleich reingehen, Manon: Felix Klein, das ist ein ziemlich bekannter Name in der Mathematik. Nach ihm sind Preise benannt, ein Mathezentrum und zwei Hörsäle in Düsseldorf und in Leipzig. Ja, und das nicht ohne Grund. Also Klein hat viel dazu beigetragen, vor allem zur Geometrie, aber auch zur Pädagogik zum Beispiel, also wie man Mathe an Schulen und an der Uni vermitteln sollte. Aber mit Abstand am berühmtesten ist ein mathematisches Objekt, das Klein sich sozusagen ausgedacht hat, nämlich die Kleinsche Flasche. Ich habe diese Flasche ja auch schon mal live gesehen, vor ein paar Wochen, als wir hier in Leipzig zu dritt auf einer Mathe-Veranstaltung zu Ehren Kleins waren. Du und Demian, ihr wart so: „Boah, guck mal Caro, die berühmte Kleinsche Flasche!“ Und ich war ehrlich gesagt erstmal ein bisschen underwhelmed, weil als echte Flasche taugt die Kleinsche Flasche nicht wirklich. Die sieht halt eher aus wie so ein Designobjekt, das aber keinen richtigen Nutzen hat. Ja, ich weiß, was du meinst. Also in Leipzig ist mir ehrlich gesagt auch zum ersten Mal aufgefallen, dass die jetzt gar nicht so besonders aussieht. Aber das ist wirklich eine besondere Flasche, also mathematisch gesehen. Da braucht man aber schon noch ein bisschen Kontext, um das zu checken. Weil, ja, wenn man jetzt nicht gerade total geometriebegeistert ist, dann checkt man es halt eher nicht. Ja, streng genommen ist es ja auch gar keine Flasche. Also das hast du ja auch schon erkannt. Man kann zwar theoretisch was reinfüllen, aber das ist halt nicht ihr Zweck. Das sieht man auch ziemlich schnell. Denn das Besondere an der Kleinschen Flasche ist, dass sie kein Innen und kein Außen hat. Also wenn überhaupt, denn es ist eigentlich sogar eine vierdimensionale Flasche und keine dreidimensionale. Aber ich habe ja dieses flaschenähnliche Ding mit meinen eigenen Augen gesehen. Das war ja ganz offensichtlich dreidimensional. Ja, also die Kleinsche Flasche wird sehr viel sogar in 3D gebaut. Aber sie ist halt eigentlich schon 4D. Ich sag ja, das ist eine coole Flasche, beziehungsweise ein cooles geometrisches Objekt, das seltsamerweise den Namen Flasche trägt. Also darauf kann ich mich einlassen. Später also mehr zu Kleins und Manons cooler Flasche. Aber Demian, jetzt erst mal mehr zu Kleins aufregendem Leben. Also Caro, geboren wird Klein am 25. April 1849. Ein Datum, von dem Klein selbst immer wieder ganz begeistert erzählt. Denn es freut ihn so richtig, dass er an diesem 25.04.1849 Geburtstag hat. Jetzt frage ich mich gerade, ob an dem Tag irgendwas krasses Historisches passiert ist. Also außer dass Felix Klein geboren wird. Habe ich da eine Bildungslücke oder was ist das Besondere an dem Datum? Ja, also irgendwas historisch Wichtiges ist da bestimmt passiert. Aber darauf will ich nicht wirklich hinaus, sondern auf was anderes. Wenn du dir das Datum genauer anschaust, dann sind das 25.04.1849. Das sind drei Quadratzahlen. Also 25 ist 5 mal 5, klar, 4 ist 2 mal 2, und 1849, was ist dann? 43 mal 43. Jetzt hast du es mir schon verraten. Dabei war ich wirklich so kurz davor, darauf zu kommen. Aber na gut, als Mathematiker ist es ja tatsächlich ein ganz cooler Funfact zum Geburtstag. Das sehe ich ein. Ja, oder? Also man merkt halt, dass Klein ein typischer Mathematiker ist, der sich über solche kleinen Gimmicks freut. Und überhaupt mag er alles, was irgendwie unterhaltsam ist. Das ist auch sein Motto als Mathematiker, was er immer wieder betont: Sei niemals langweilig. Na, hoffentlich hat er genug spannende Storys auf Lager. Nicht, dass der dann der Typ ist, der in die Kneipe reinkommt und sagt: „Hey Leute, habe ich euch schon erzählt, an was für einem bemerkenswerten Datum ich geboren wurde?“ Und alle so: „Ja, Felix, ungefähr schon 100 Mal.“ Die Geschichte schon wieder? Ne, ne, also das wäre natürlich blöd. Aber an sich kann ich ihn gut verstehen. Also meine Personennummer in Argentinien zum Beispiel, das war eine Aneinanderreihung von Zweierpotenzen, und das finde ich auch ziemlich cool, muss ich sagen. Also jetzt möchte ich eigentlich aus Prinzip mir auch gleich mal mein Geburtsdatum, meine Personennummer, meine Steuer-ID, das weiß ich nicht alles ganz genau anschauen und gucken, ob ich da auch irgendwas entdecke. Aber mal unabhängig davon, wie spannend man das jetzt findet, dass Klein sich so für sein Geburtsdatum begeistert, das klingt jetzt erstmal so gar nicht nach Drama, finde ich. Also ich versuche mir vorzustellen, wie dieser Typ, der gerne von seinem Quadratzahlen-Geburtstag erzählt, wie der auf einmal zur Hauptfigur im Game of Thrones der mathematischen Denkschulen wird. Ja, das fragt sich Klein wahrscheinlich selbst damals auch ein paar Mal. Das ist eigentlich ein recht netter Typ, würde ich sagen, dieser Felix Klein. Aber er ist halt Mathematiker zu einer Zeit, als es gerade ein großes Battle zwischen zwei Städten gibt. Oder besser gesagt, zwischen zwei Unis, zwei Denkschulen: Berlin und Göttingen. Das Game of Thrones der Mathematik ist also Haus Berlin gegen Haus Göttingen. Ja, genau, kann man so sagen. Jedes Haus hat seine eigene goldene Generation: Berühmte Mathematiker, die wie in Teams gegeneinander antreten, könnte man schon sagen. Das geht 1800 schon los. Das sind in Göttingen Karl Friedrich Gauss, Heinrich Weber und Moritz Stern. Und in Berlin Peter Gustav Dirichlet, Jakob Steiner und Karl Gustav Jakob Jacobi. Dann kommt die nächste Generation: In Göttingen Bernhard Riemann, Alfred Clebsch, Hermann Armandus Schwarz. In Berlin Ernst Kummer, Karl Weierstrass und Leopold Kronecker. Okay, und dann kommt Felix Klein. Ja, und Klein ist ein besonderer Typ Mathematiker. Schon immer gibt es Mathematiker, die wollen halt forschen und sonst nichts. Die wollen nicht unterrichten, die wollen keine Schule, und die wollen auf gar keinen Fall irgendwas mit Papierrahmen zu tun haben. Und Klein ist da das komplette Gegenteil. Klein liebt das alles, diese ganzen Hochschul-Politics: Wer geht an welche Uni, wer hat welche Schüler, was machen die in welcher Fachzeitschrift, haben die schon publiziert. Er ist sehr gut im Networken, und diese Info hilft ihm auch dabei. Heute ist Felix Klein ja vor allem auch als Pädagoge bekannt. Er denkt viel darüber nach, wie man mathematisches Wissen zum Beispiel auch an der Schule vermitteln kann. Ja, Klein hat überall seine Finger im Spiel. Aber auch irgendwelche coolen 3D-Modelle für den Matheunterricht. Dann gibt er in Göttingen eine berühmte Fachzeitschrift heraus. Dann will er eigentlich Physik machen oder Technik. Dann schreibt er wieder tausend Briefe mit wichtigen Mathematikern über Mathe, natürlich, aber auch über alles andere. Ob irgendwelche Schüler von ihm nicht vielleicht an dieser oder jener Uni unterkommen könnten. Also er ist wirklich total umtriebig. Okay, jetzt hast du ja schon diese tausend Namen aufgezählt, die irgendwie in diesem Battle Berlin-Göttingen mit drin hängen. Wie ist Klein da jetzt mit drin verwickelt und was bedeutet das überhaupt? Da sitzen die Göttinger zusammen und lästern über die Berliner. Also ich glaube, das ist ein kleines bisschen so, ja. Also es geht dabei natürlich um grundverschiedene Überzeugungen und Arbeitsweisen und Forschungsschwerpunkte. Aber ja, die ziehen schon übereinander her. Die Berliner sagen zum Beispiel, die Göttinger sind so unordentlich, so sloppy. Die stecken mit dem Kopf in ihren komischen geometrischen Modellen und dann reden die über irgendwelche Anwendungen. Und nie wird irgendwas mal schön sauber ordentlich aufgeschrieben. Das ist eigentlich keine richtige Mathematik. Und die Göttinger? Die Göttinger sagen, die Berliner, die sind total unkreativ. Die machen die ganze Zeit nur Logik, total streng, total konservativ. Wie so Mathemaschinen, die können ja überhaupt nicht so richtig frei denken. Ich seh schon, sei niemals langweilig und so. Ja, genau, das Motto passt natürlich gar nicht zu dem Konservativen da in Berlin. Da ist zum Beispiel Karl Weierstrass, ein ganz berühmter Mathematiker aus Berlin. Da gibt es heute noch den Ausdruck „Weierstrasssche Strenge“, wenn man etwas super duper penibel genau machen will. Ich hätte ja gedacht, MathematikerInnen machen grundsätzlich Dinge eh sehr gern sehr genau. Aber ich nehme mal mit, die Berliner sind da besonders neurotisch. Und die Göttinger denken, sie wären die coolsten und alle anderen sind halt total langweilig. In Berlin sieht man die Schönheit der Mathematik, würde ich sagen, eher in der Rigorosität. Und Göttingen stattdessen in der Intuition. Okay, ich will mir da jetzt gar kein Urteil bilden. Hat bestimmt alles so seine Vorzüge. Das ist ja vielleicht auch einfach ein bisschen eine Typfrage. Aber Mini-Exkurs: Sowohl Charlotte, meine Kollegin und hier aktuell stille Redakteurin im Hintergrund bei diesem Podcast, die hat in Berlin Logik studiert, und ich finde die eigentlich gar nicht langweilig. Und du, Demian, du bist ja jetzt auch am Institut für Mathematik an der Humboldt-Uni in Berlin. Und naja, du hast auf jeden Fall viele spannende Mathe-Geschichten auf Lager. Also meine Erfahrung mit Berliner Mathe-Menschen ist positiv, und meine Erfahrung mit Göttinger Mathe-Menschen ist nicht vorhanden. Also meine anekdotische Evidenz sagt 1 zu 0 für Berlin. Also wobei in Berlin zum Beispiel lange Zeit keine Frauen promovieren durften. Das war generell so in Deutschland damals. Die sind dann eher zu Klein nach Göttingen gegangen, weil er sich damals dafür eingesetzt hat, dass sie das tun können. Also da sind sehr coole Mathematiker da in Berlin. Menschlich bin ich im neunzehnten Jahrhundert zumindest schon eher Team Göttingen, muss ich sagen. Ist ja zum Glück auch alles nicht so ernst gemeint. Also hoffentlich fühlt sich jetzt kein Mathematiker oder keine Mathematikerin aus Göttingen auf die Füße getreten. Ihr seid auch cool und kreativ und intuitiv. Das lieben wir doch. Aber genug davon. Jetzt können wir ja nicht dieses ganze Berlin-Göttingen-Battle nacherzählen. Das zieht sich ja auch über ein gutes Jahrhundert oder so, diese Rivalität. Aber vielleicht kannst du ja mal konkret erzählen, wie lästern die denn damals übereinander? Es gibt unglaublich viele Geschichten, wie die sich gegenseitig ärgern und so kleine Gemeinheiten übereinander sagen. Ich habe mal eine Geschichte rausgesucht, die ganz gut zeigt, wie Klein da überhaupt reingerät. Da ist Klein noch Professor in Leipzig. Moment, Moment! Wieso Leipzig? Ich dachte, das ist Berlin gegen Göttingen. Ja, also du kannst damals auch Team Göttingen sein, ohne in Göttingen zu sein. Hauptsache, du bist für Riemann. Das war, sagen wir mal, Dreh- und Angelpunkt in Göttingen. Alles andere ist egal. Team Göttingen ist einfach nur Team Riemann. Und gegen den strengen Weierstrass natürlich voll gegen Weierstrass und Kronecker und Kummer, diese ganzen Langweiler aus Berlin. Okay, also Klein ist zwar nicht in Göttingen, aber er ist im Team Göttingen. Ja, genau. Klein hat schon auch Bezüge nach Göttingen. Seine größten Unterstützer sind in Göttingen. Und dann dauert es auch nicht mehr lange: 1886 geht Klein auch als Professor nach Göttingen. Aber 1881, da sitzt Klein noch in Leipzig und forscht gerade zu einer bestimmten Klasse an Funktionen. Die Idee dazu, die kommt natürlich von Riemann, und dann hat Schwarz noch was dazu geforscht. Und jetzt eben Klein. Also man kann schon sagen, das halbe Team Göttingen hängt da mit drin. Jetzt sitzt Klein da zu Hause an seinem Schreibtisch und liest drei neue Artikel aus Frankreich, dieses Mal von Henri Poincaré: Sur les fonctions fixées. Aha, also was Neues von einem dieser Berliner Mathematiker, Lazarus Fuchs. Klein findet das alles ganz interessant. Er macht sich Notizen: Das könnte man anders machen, hier fehlt vielleicht noch was, und hier kann ich was ergänzen. Und dann merkt er: Moment mal, es geht da eigentlich um die Funktionen, an denen Riemann, Schwarz und eben er selbst schon gearbeitet haben. Oh oh. Oh oh, ne. Diese Funktionen sollen jetzt Fuchs’sche Funktionen heißen, eben nach Lazarus Fuchs benannt. Und in den Artikeln gar kein Wort über Riemann, über Schwarz und auch kein Wort über Felix Klein. Und was macht er? Der nimmt einen Stift und schreibt seinen eigenen Namen hinzu: Sur les fonctions kleiniennes. Okay, Klein ist offensichtlich not amused, dass der Fame an Lazarus Fuchs geht, beziehungsweise an einen Mathematiker aus der Berliner Schule. Ist das jetzt ein klassischer Fall von Ideenklau? Hat Poincaré das einfach vercheckt? Oder hat Klein hier eine verschobene Wahrnehmung und die Funktionen kommen in Wirklichkeit echt von Fuchs? Eigentlich ein bisschen was von allem. Klein hat hier schon einen Punkt, finde ich. Die Credits gehen halt komplett an Fuchs, weil Poincaré halt nur Fuchs kannte. Aber Klein findet das natürlich einfach unfair. Jedenfalls schreibt Klein direkt einen Brief an Poincaré: „Sorry, aber das sind meine Funktionen, nicht die von Fuchs.“ Ziemlich genau das. Er schreibt: „Ich protestiere gegen den Namen Fuchs’sche Funktionen.“ Und er schreibt, dass die Idee ja von Riemann kommt, dass Schwarz natürlich sehr viel dazu gearbeitet hat und nicht zuletzt eben er selbst. Und Fuchs? Ja, das liest sich besonders schön. Also was den Herrn Fuchs angeht, der hat sich wohl auch einmal mit ähnlichen Fragen befasst, und er hat nur eins geschafft, so Klein: „Uns zu zeigen, dass er absolut nichts davon versteht.“ Oha. Und was antwortet Poincaré? In unserer Geschichte aus der Mathematik haben wir den ja eigentlich mal als ziemlich korrekten Typen kennengelernt, der seine Fehler auf jeden Fall korrigieren will. Also ist der jetzt so: „Oh, sorry, mein Fehler, das sind natürlich Riemann, Schwarz, Klein’sche Funktionen.“ Die Antwort von Poincaré ist ziemlich berühmt. Er schreibt nämlich in diesem Briefwechsel einen einzigen Satz auf Deutsch: „Namen sind Schall und Rauch.“ Oh Mann, wie unfair. Ja, da muss ich wohl mein Bild von ihm noch ein bisschen korrigieren. Poincaré kann halt jetzt nicht wirklich zurückrudern, ohne Fuchs vollkommen zu blamieren. Und Poincaré selbst baut seine eigenen Arbeiten auf denen von Fuchs auf, sodass für ihn Poincaré der Name auch gerechtfertigt ist. Okay, ein Punkt für Berlin, würde ich sagen. Wie geht die Geschichte denn weiter? Also wer gewinnt am Ende diesen Machtkampf? Naja, also diese Fuchs-Geschichte ist natürlich hier noch nicht zu Ende. Erstmal kommt Poincaré nochmal und sagt: „Ja, okay, hier gibt es ja noch ein paar andere schöne Funktionen. Lass mal die Klein’schen Funktionen benennen, bitte schön.“ Dann gibt es einen Schüler von Klein, Adolf Hurwitz. Der will sich halt ein bisschen über Fuchs lustig machen wegen dieser ganzen Affäre. Und er findet dazu ein kleines Lied: „Fuchs, du hast die Funktion gestohlen, gib sie wieder her, gib sie wieder her.“ Oh Mann, ey, eine sehr erwachsene Konfliktkommunikation unter sehr erwachsenen Männern. Als ob Frauen immer sehr erwachsen Konflikte lösen würden. Okay, allerdings sind die Berliner auch nicht besser. Also Kronecker stirbt, rest in peace. Man muss sich vorstellen, da ist diese Geschichte schon mehr als zehn Jahre her. Da muss in Berlin natürlich seine Professur neu besetzt werden. Und die kommen da auch in Berlin nicht dran vorbei, auch mal über Klein zu reden, so als Kandidaten. Das Problem ist nur, in dieser Berufungskommission da sitzt auch ein gewisser Lazarus Fuchs. Und der sagt: „Also ich habe ja eigentlich nichts persönlich gegen Klein. Na klar, natürlich nicht. Ich habe nur etwas vorzubringen gegen sein verderbliches Vorgehen auf wissenschaftlichem Gebiet.“ Ich nehme mal an, Klein wird dann eher nicht nach Berlin berufen. Nein, natürlich nicht. Weierstrass soll dann noch gesagt haben, dass Klein ja eh ein Blender ist. Also niemand will Klein hier in Berlin haben. Für Göttingen ist das natürlich ein Glücksfall. Denn am Ende gewinnt Göttingen diesen Machtkampf mit Berlin. Und zwar vor allem wegen Klein. Weil Klein dann als Mathematiker in Göttingen so wichtig wird. Nein, ehrlich gesagt ist Klein damals als Mathematiker gar nicht mehr so aktiv. Aber Klein macht am Ende den alles entscheidenden Move. Er holt nämlich einen echten Superstar nach Göttingen: David Hilbert. Damian, das ist jetzt bestimmt schon der tausendste Name in dieser Geschichte. Langsam reicht’s. Aber hey, immerhin ist das mal ein Name, der hier auch schon mal das ein oder andere Mal im Podcast vorgekommen ist. Das ist der Mathematiker, der auf dem Mathematikerkongress in Paris diese Liste mit den größten ungelösten Matheproblemen vorgestellt hat. Ja, genau. Hilbert ist einfach Next Level, der absolute Endgegner. Und das ist halt jetzt wirklich die goldene Generation in Göttingen: Klein und Hilbert. Dazu kommen noch Herbert Minkowski und später dann noch Emmy Noether. Team Göttingen hat also die Nase vorn. So ist es. Damals ist Hilbert, was die Mathematik angeht, wirklich so ziemlich unschlagbar. Und das hat Göttingen wiederum auch Felix Klein zu verdanken. Wenn wir hier im Podcast jetzt gleich genauer auf die Mathematik schauen, dann wäre es natürlich naheliegend, jetzt mal zu gucken, was es mit den fuchsischen beziehungsweise Riemann-Schwarz-Klein’schen Funktionen auf sich hat. Aber ich habe mich überzeugen lassen: Wer über Felix Klein redet, der muss über die Kleinsche Flasche reden. Es geht einfach nicht anders. Ich bin ja, wie ihr schon wisst, Kleinsche Flaschen-Skeptikerin. Aber ich dachte mir: Hey, was soll’s, ich lasse mich auch gerne vom Gegenteil überzeugen. Ich habe hier vor mir die offizielle Beschreibung der Kleinschen Flasche durch Felix Klein, die da lautet: „gewisse unberandete Doppelflächen.“ Okay, man kann sich von denselben ein Bild machen, indem man etwa ein Stück eines Kautschukschlauches umstülpt und nun so sich selbst durchdringen lässt, dass bei Zusammenbiegung der Enden die Außenseite mit der Innenseite zusammenkommt. Hm, okay, ich sehe es ein. Das kann ich mir jetzt auch nicht so wahnsinnig gut vorstellen. Also vielleicht nochmal von vorne: Was ist die Kleinsche Flasche? Lass uns vielleicht noch weiter vorne anfangen und zwar mit einem Gürtel. Okay, na gut, soweit kann ich zumindest folgen, und ich habe da natürlich was vorbereitet. Okay, man muss fangen. Oh, okay, wir haben einen Gürtel. Wir haben hier einen Gürtel, und den kannst du jetzt einfach ganz normal zumachen. Und jetzt hast du einen geschlossenen Kreis. Also du hast zwei Seiten: außen hier die glatte Lederfläche und innen Wildleder. Okay, soweit so gut. Es gibt zwei Seiten, also das ist jetzt wirklich wichtig, weil wenn du jetzt außen mitten auf die Schnalle so eine Ameise setzt und die läuft jetzt geradeaus los, dann kann die tausendmal im Kreis um diesen Gürtel drumrumlaufen, aber die bleibt halt einfach immer außen. Ja, wenn es eine sehr erfolgreiche Ameise ist, die wirklich immer geradeaus läuft, dann ja, okay. So, und jetzt machst du den Gürtel aber nochmal zu, aber bevor du den zumachst, drehst du das eine Ende einmal um 180 Grad. Also du ziehst den Gürtel sozusagen falsch durch die Lasche. Ja, es sieht ein bisschen falsch aus, aber okay. Ja, da ist jetzt so ein halber Twist drin in diesem Gürtel, und die Frage ist: Gibt es jetzt immer noch einen außen? Also was passiert, wenn die Ameise jetzt losläuft? Okay, die Ameise läuft da einmal so halb außen rum, und dann macht der Gürtel halt einen Twist. Und ja, okay, jetzt ist die Ameise vielleicht eher innen. Ja, und jetzt mach mal weiter. Okay, dann kommt die Ameise da wieder an der Schnalle an, nur diesmal halt innen, und dann geht es wieder einmal innen rum und dann kommt wieder der Twist. Genau, diesmal von innen nach außen. Aha, also die Ameise läuft quasi immer im Kreis, aber sie läuft dabei immer einmal außen rum und dann einmal innen rum, weil sie ja quasi beim Twist immer die Seite wechselt. Genau, es gibt quasi kein innen und kein außen, beziehungsweise in der Mathematik sagt man, das ist nicht orientierbar. Kein innen, kein außen, kein oben, kein unten. Und das, was wir gerade hier mit diesem Gürtel gebastelt haben, das ist ein Möbiusband. Ah, ein Twist in einem Band, und schon ist es eine mathematische Entdeckung. Nice! Naja, das eine ist es herzustellen, und das andere ist es, das wirklich mathematisch zu beschreiben. Ja gut, das ist ein kleiner Unterschied vielleicht. Aber ja, wie die Kleinsche Flasche wirkt, auch das Möbiusband auf den ersten Blick jetzt nicht wirklich spektakulär. Und es ist uns wahrscheinlich auch schon zigmal im Alltag begegnet, also wenn man jetzt zum Beispiel den Gürtel falsch zuschneidet. Aber erinnerst du dich zum Beispiel noch an diese Schals, die es mal gab? Also zu der Zeit, als wir ungefähr Abi gemacht haben, da gab es immer diese Infinity-Schals, also Schlauchschals, die einmal in sich selbst so verdreht sind. Jaja, also so einen Loop-Schal, den hatte meine Schwester auf jeden Fall auch. Die war nämlich ein bisschen cooler als ich und wusste auch, wie man sowas richtig trägt, dass es auch lässig aussieht. Ja, ich hatte ungefähr so 20 davon. Du warst so lässig. Das habe ich nicht gesagt. Und es gibt auch so eine Bahn bei Mario Kart, also Mario Kart 8. Das ist auch ein Möbiusband. Ja, ich habe auf jeden Fall noch nie so über diese Schals oder über die Mario Kart-Bahn nachgedacht, dass es da kein Innen und kein Außen gibt. Unter diesen neuen Gesichtspunkten ist es schon ein cooles Phänomen. Aber ein Möbiusband ist ja jetzt keine Kleinsche Flasche. Also was hat Klein jetzt mit dem Möbiusband zu tun? Wie hängt das zusammen? Was Klein gemacht hat, ist, er hat sich überlegt, was passiert, wenn ich jetzt zwei Möbiusbänder nehme und die dann am Rand zusammenklebe. Also wenn man zwei Gürtel am Rand zusammenklebt, dann kriegt man einfach einen Gürtelschlauch. Ja, aber was passiert, wenn man jetzt zwei Möbiusgürtel zusammenklebt? Das klingt nach ziemlichem Kuddelmuddel. Aber ja, keine Ahnung, was passiert dann? Sag’s mir. Es geht nicht. Ja gut, dann probiere ich das zu Hause auch gar nicht erst aus. Also es geht nicht in unserer dreidimensionalen Welt. Du kannst es also nicht basteln. Also es geht halt wirklich nicht. Aber rein mathematisch gesehen geht es halt schon. Also mathematisch kannst du zwei Möbiusbänder zusammenkleben. Du brauchst dafür halt einfach nur vier Dimensionen. Und wenn du das machst, also wenn du zwei Möbiusbänder mathematisch zusammenklebst, dann ist das Ergebnis Trommelwirbel: eine Kleinsche Flasche. Möbiusbänder zusammengeklebt in vier Dimensionen – das ist eine Kleinsche Flasche. Aber ich habe doch eine Kleinsche Flasche mit meinen eigenen Augen gesehen, in echt, also in 3D. War das dann eine Kleinsche Flasche oder war das dann eigentlich keine Kleinsche Flasche? Jein. Also die Frage ist, was passiert, wenn man das in der dreidimensionalen Welt ähnlich zusammenbastelt? Also wir haben doch gesagt, bei Möbiusbändern gibt es immer diesen Twist. Der Gürtel dreht sich einmal halb um sich selbst. Und wenn man jetzt zwei davon zusammenklebt, dann dreht sich auch genau das zusammengeklebte Ergebnis einmal in sich selbst rein und wieder aus sich raus. Ja, okay. Also ich kann es mir jetzt so grob vorstellen, weil ich diese Kleinsche Flasche noch vor meinem geistigen Auge habe. Aber wer die noch nie gesehen hat, der sollte jetzt am besten einfach mal googeln. Weil ich glaube, sonst kann man sich das ungefähr so gut vorstellen wie bei Klein mit seinem Kautschukschlauch, der sich irgendwie selbst durchdringt. Also ihr könnt euch das vorstellen wie einen Elefanten. Also der Elefant hat ja einen Rüssel. So, und der Rüssel, der ist ja hohl und wäre normalerweise der Flaschenhals. Aber der Kleinsche Elefant hat da keine Öffnung, weil der Kleinsche Elefant steckt seinen Rüssel in den Mund. Ich bin gespannt, worauf das hinausläuft. Ja, okay. Und es tut mir leid, das wird jetzt vielleicht ein bisschen eklig in der Vorstellung, aber der Rüssel wird jetzt zum Darm. Und der Rüssel geht vom Mund einmal komplett durch den Elefanten durch und kommt dann hinten wieder raus. Und das ist die Kleinsche Flasche – kein Innen und kein Außen. Okay, gut, das ist quasi ein Kleinscher Elefant. Also der Elefantenrüssel stößt sich nach innen und dann stößt sich dieser Rüsselschlauch hinten wieder nach außen. Genau. Also das Besondere an der Kleinschen Flasche ist ja, dass es eben kein Innen und kein Außen gibt, so wie beim Möbiusband. Ja, das kann man sich jetzt genauso vorstellen wie beim Möbiusband. Also wieder mit der Ameise. Die Ameise hat Pech gehabt und ist im Elefantenrüssel drin. Also sie ist jetzt innen, innen im Rüssel. Und jetzt läuft sie innen im Rüssel entlang und durch diesen Rüsselschlauch einmal durch den Elefanten durch und dann hinten wieder raus. Dann kann sie schön außen auf dem Elefanten wieder nach vorne krabbeln und sich dann schön auf den Rüssel setzen. Und dann ist sie außen. Ja, genau, dann ist sie außen, obwohl sie ja nur geradeaus gelaufen ist. Und das ist halt das Besondere an der Kleinschen Flasche oder am Kleinschen Elefanten. Ich meine, wenn eine Ameise in einem Luftballon rumkrabbelt, dann ist sie ja nicht plötzlich einfach außen auf dem Luftballon drauf. Mathematisch würde man sagen, der Luftballon ist orientierbar und die komplette Kleinsche Flasche ist nicht orientierbar. Und das ist dann schon irgendwie cool. Ja, oder? Und in 4D ist es halt nochmal viel cooler, weil da geht der Rüssel gar nicht erst durch den Elefanten durch und macht auch gar nicht sowas. Also in 4D, muss ich sagen, bin ich wieder ein bisschen lost. Da kommt meine Vorstellungskraft echt an ihre Grenzen. Ja, keine Sorge. Also niemand kann sich vier Dimensionen vorstellen. Was man sich aber vorstellen kann, ist zum Beispiel den Schatten vom Elefanten. Ja, das kann ich. Und weiter. Wenn der jetzt seinen Rüssel neben seinen Mund steckt, dann ist er ja nicht im Elefanten, sondern daneben. Aber auf dem Schatten kann man das ja eben nicht sehen. Also auf einem zweidimensionalen Schatten sieht es so aus, als würde der Rüssel straight in den Elefanten reingehen. Ja, stimmt. Und so ähnlich ist es beim Kleinschen Elefanten auch. Der Rüssel geht gar nicht wirklich durch ihn durch, aber in 3D kann man das halt eben nicht sehen. Also das, was ich gesehen habe, dieses 3D Modell von der Kleinschen Flasche, das ist sowas wie der dreidimensionale Schatten von einer echten Kleinschen Flasche. Kann man so sagen? Ja, okay. Also jetzt finde ich die Kleinsche Flasche doch ziemlich spannend, so mit Kontext als Eingeweide. Was mich jetzt zum Schluss aber noch interessieren würde, Demian, Manon, ihr kommt ja aus der Mathematik beziehungsweise aus der Physik. Wie war das denn bei euch mit der Kleinschen Flasche? Sieht man sowas dann und denkt sich sofort: Wow, eine nicht orientierbare vierdimensionale Flasche, wie cool? Ja, absolut. So ähnlich, ja. Also jetzt mal ernsthaft gesprochen, ich denke, die Kleinsche Flasche kann sehr gut als eine kleine Warnung dienen, in der Mathematik nicht immer unserer Intuition zu vertrauen. Ganz oft gehen wir nämlich von Sachen aus, die so gar nicht wirklich stimmen. Ich meine zum Beispiel, hätte ich persönlich intuitiv gedacht, dass jede geschlossene Fläche so wie eben eine Kugel oder ein Donut eben immer eine Innen- und eine Außenseite hat. Also alle Flächen, die ich mir so vorstelle, sind halt so. Das ist aber halt nicht wahr, wie wir heute gesehen haben. Und in der Mathematik ist es unglaublich wichtig, nie von etwas auszugehen, nur weil die eigene Erfahrung oder Intuition das nahelegt. Also ja, die Kleinsche Flasche ist für mich eine Warnung, dass die Mathematik das macht, was sie eben will, und wir Menschen eigentlich nur zuschauen dürfen und das dann beschreiben. Genau. So philosophisch werde ich mich jetzt nicht äußern, tut mir leid. Also ich muss sagen, aus physikalischer Sicht ist die Kleinsche Flasche tatsächlich auch ziemlich cool, vor allem in der Quantenphysik. Weil da gibt es nämlich so eine Idee, dass Elektronen verschiedene Spindzustände haben können. Das sind so magnetische Eigenschaften von Teilchen. Und die stellt man sich oft wie so einen Pfeil vor, den die Teilchen mit sich rumtragen. Also wie so ein kleiner Stabmagnet, der mal nach oben oder mal nach unten zeigen kann. Und diese Spindzustände, die verhalten sich halt mega kontraintuitiv. Also wenn man diesen Pfeil einmal komplett um 360 Grad dreht, dann zeigt er nämlich plötzlich einfach in die entgegengesetzte Richtung. What? Ja, das kann man sich eigentlich gar nicht vorstellen. Aber wenn man sich so ein Möbiusband nimmt, dann wird es doch verständlich. Weil das ist ja wie diese Ameise. Wenn die einmal rumgelaufen ist, dann ist sie ja auf der anderen Seite vom Band gelandet. Und wenn die Ameise jetzt ein Pfeil ist, der anfangs nach oben zeigt, dann zeigt der Pfeil nach 360 Grad halt eben nach unten. Und mit der Kleinschen Flasche funktioniert das auch. Also halt nicht mit dem Spin, sondern das ist alles ein bisschen komplizierter mit den Quantenzuständen. Aber da taucht es auch auf. Okay, ja, spannend. Aber bevor es hier gleich noch komplizierter wird, machen wir den Sack vielleicht mal zu für heute. Ja, das war unsere Geschichte aus der Mathematik über Felix Klein, die ewige Rivalität zwischen Berlin und Göttingen und eine Flasche, die es heute wahrscheinlich in jede einzelne Mathe-Uni auf der ganzen Welt geschafft hat. Ja, diese Geschichte hat angefangen mit dem Geburtstag von Felix Klein und sie soll hier mit seinem Todestag enden, beziehungsweise mit seinem Todesjahr. Felix Klein ist nämlich im Jahr 1925 gestorben, was leider keine Quadratzahl ist. Aber immerhin bedeutet das, dass wir in diesem Jahr dem 100. Todestag von Felix Klein gedenken. Und er hätte sich bestimmt gefreut. 2025 ist nämlich eine Quadratzahl: 45 mal 45. Jedenfalls anlässlich des 100. Todestags von Klein in diesem Jahr waren Manon, Demian und ich bei den DMV Topic Days Felix Klein in Leipzig. Das war eine Veranstaltung zu Felix Klein, zu der die DMV, also die Deutsche Mathematikervereinigung, und das Max-Planck-Institut für Mathematik in den Naturwissenschaften eingeladen haben. Dort haben wir uns Vorträge über Klein angehört und Demian hat ein Interview der etwas anderen Art geführt. Mehr dazu gibt es hier an dieser Stelle in zwei Wochen, am 31. Dezember, also an Silvester. Aber erstmal schöne Weihnachten euch allen! Frohe Weihnachten! Frohe Weihnachten! Geschichten aus der Mathematik ist eine Kooperation vom Podcast Radio detektor.fm und Spektrum der Wissenschaft. Die Idee für den Podcast und die Story kommen von Denia Nauwe Goos. Die Mathematik erklärt Hartmannor Bischoff. Die Redaktion für diese Folge hat Charlotte Thielmann übernommen. Die Musik kommt von Tim Schmutzler. Die Folge produziert hat Stanley Baldauf. Und die Moderation kommt von mir, Caroline Breitschädel. Alle Folgen findet ihr auf detektor.fm und spektrum.de. Also der Elefant hat einen Rüssel. So, und normaler. Und der Rüssel – der Elefant hat einen Rüssel. Ich habe noch nie in meinem Leben so oft gesagt, dass ein Elefant einen Rüssel hat. Ich weiß auch nicht, ob ich es genau verstanden habe. Meinst du, der hat einen Rüssel? Jetzt gleich zeigt Demian wieder das komische Meme. Der Elefant hat nämlich zwei Rüssel. Demians Meme. Das hast du. Du hast jetzt aber noch nicht aufgenommen, oder? Hoffe ich. Das lösche ich alles. Outtakes. Ganz weirde Outtakes mit den Folgen zu tun.
 Foto: Spektrum der Wissenschaft
Foto: Spektrum der Wissenschaft Foto: Chris Coe
Foto: Chris Coe